冒泡排序(Bubble Sort)
冒泡排序只会操作相邻的两个数据,每次冒泡操作都会对相邻的两个元素进行比较,如果比较条件不满足就让它俩互换位置,
一次冒泡会让至少一个元素移动到它应该在的位置,重复n次就可以让n个数据有序排列
举个例子
比如要对[1,11,88,5,32]这几个元素按照从小到大的顺序排列,该怎样排序呢?
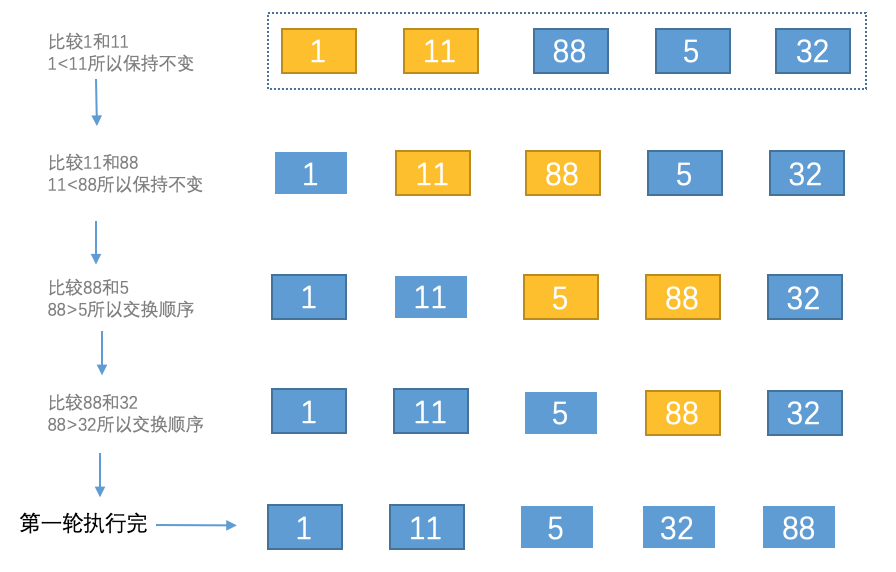 经过上述第一轮操作,那么我们已经把这个数组中的最大元素位置放好了,
经过上述第一轮操作,那么我们已经把这个数组中的最大元素位置放好了,88在数组中最大,所以放在最后一位
然后我们重复执行,依次排序即可得到结果, 用swift实现:
/// 冒泡排序
/// - Parameter nums: 数组
func bubbleSort(nums: inout [Int]) {
let n = nums.count
for i in 0..<n {
for j in 0..<(n - 1 - i) {
if nums[j] > nums[j + 1] {
nums.swapAt(j, j + 1)
}
}
}
print(nums)
}
var nums = [1,11,88,5,32]
bubbleSort(nums: &nums) // 输出:[1, 5, 11, 32, 88]
冒泡排序思想是:
- 从头开始比较
相邻两个元素的大小,如果第一个比第二个大,就交换这两个元素的位置 - 第一轮执行完之后,那么最后一个元素就是最大的
- 忽略上一步中找到的那个最大元素,重复执行步骤一,直到全部元素有序
冒泡排序的优化(一)
在冒泡排序一些特定数据时,当某次冒泡操作已经没有数据交换时,说明已经达到完全有序,不用再执行后序的冒泡操作了
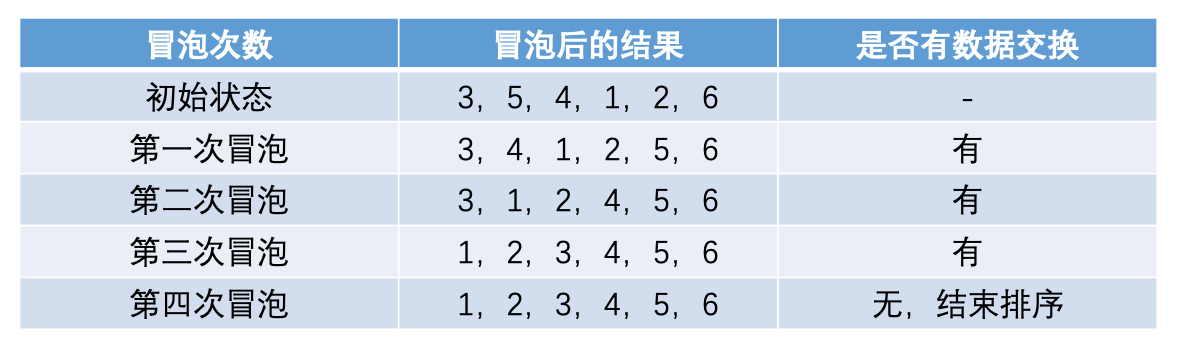 优化过后的冒泡排序:
优化过后的冒泡排序:
/// 冒泡排序
/// - Parameter nums: 数组
func bubbleSort(nums: inout [Int]) {
let n = nums.count
for i in 0..<n {
var sorted: Bool = false // 用于标记是否进行过排序
for j in 0..<(n - 1 - i) {
if nums[j] > nums[j + 1] {
nums.swapAt(j, j + 1)
sorted = true; // 此轮循环进行过排序
}
}
if !sorted {
break
}
}
print(nums)
}
var nums = [1,2,3,4,5,7,6]
bubbleSort(nums: &nums)
这种优化如果数据不是
完全有序,此优化会因每次都需要判断是否有交换数据而导致复杂度变大.
冒泡排序的优化(二)
如果序列尾部已经局部有序,可以记录最后一次交换的位置,减少比较次数
举个例子:
数组:[1,11,2,5,132,33,3,4,234,333,444,555,666]
第一次冒泡到达234的前一个元素时候就没有发生交换数据了,实际上后面的数据段就无须在冒泡了
其实质上是记录上一次循环最后一次交换的位置,将其作为下一次循环的截止位置。
func bubbleSort(nums: inout [Int]) {
var count = nums.count-1;
for _ in 0..<(count) where count > 1 {
var sortedIndex = 1;
for j in 0..<(count) where count > 0 {
if nums[j] > nums[j + 1] {
nums.swapAt(j, j + 1)
sortedIndex = j;
}
}
count = sortedIndex;
print("循环了一次")
}
print(nums)
}
var nums = [1,11,2,5,132,33,3,4,234,333,444,555,666]
bubbleSort(nums: &nums)
这样外层大循环只需要遍历5次即可结束冒泡
选择排序(Selection Sort)
从序列中找出最大的那个元素,然后与最末尾的元素交换位置。执行完一轮后,最末尾的那个元素就是最大的元素。
忽略上一步中曾经找到的最大元素,重复执行上一步, 这就是选择排序
初始化数组:
[0, -1, 3, 5, 7, 2, 44, 22, 10]
一:遍历数组,找出最大的元素,与末尾元素交换位置
[0, -1, 3, 5, 7, 2, 44, 22, 10] ——> [0, -1, 3, 5, 7, 2, 10, 22, 44]
二:忽略上一步中找到的最大元素(末尾元素), 重复执行上一步:
[0, -1, 3, 5, 7, 2, 10, 22, 44] ——> [0, -1, 3, 5, 7, 2, 10, 22, 44]
三:重复执行,得到最终排序结果
... ——> [-1, 0, 2, 3, 5, 7, 10, 22, 44]
/// 选择排序
/// - Parameter array: 要排序的数组
func selectionSort(array: inout [Int]) {
for end in (1..<array.count).reversed() {
var maxIndex = 0
for begin in 1...end {
if array[maxIndex] <= array[begin] {
maxIndex = begin;
}
}
let tmp = array[maxIndex]
array[maxIndex] = array[end]
array[end] = tmp
}
}
var array = [0, -1, 3, 5, 7, 2, 44, 22, 10]
selectionSort(array: &array)
print(array) // [-1, 0, 2, 3, 5, 7, 10, 22, 44]
插入排序(Insertion Sort)
一个有序的数组,向里面添加一个新的数据后,如何继续保持数据有序呢?
很简单,我们只要遍历数组,找到应该插入的位置将其插入即可,这就叫做插入排序算法
实现原理:
插入排序会将数据分为两个区间已排序区间和未排序区间,初始化默认已排序区间只有一个元素,就是数组的第一个元素。
插入算法的核心思想是取未排序区间中的一个元素,与已排序区间的元素依次比较大小,找到合适的位置将其插入,并保证已排序区间数据一直有序,
重复这个过程,直到未排序区间中的元素为空,算法结束
比如,数组初始化为[8, 3, 5, 4, 6] ,我们用|来区分已排序区间和未排序区间,排序过程应该是这样子:
初始化默认左侧已排序区间只有一个元素,所以是这样子的
[8 | 3, 5, 4, 6]
一:拿3和8比较,3比8小,所以3和8交换位置,得到排序序列,已排序区间元素为2
[8 | 3, 5, 4, 6] ——> [3, 8 | 5, 4, 6]
二:拿5和8比较,5比8小,所以5和8交换位置
[3, 8 | 5, 4, 6] ——> [3, 5, 8 | 4, 6]
由于已排序区间已经有两个元素了,5和8交换位置之后还需要和3再次比较,5>3,所以不需要交换位置
三:拿4和8比较,4比8小,所以4和8交换位置
[3, 5, 8 | 4, 6] ——> [3, 5, 4, 8 | 6]
再拿4和已排序区间的5比较,4<5所以4和5交换位置
[3, 5, 4, 8 | 6] ——> [3, 4, 5, 8 | 6]
再拿4和已排序区间的3比较,4>3所以不需要交换位置
[3, 4, 5, 8 | 6]
四:拿6和8比较,6比8小,所以6和8交换位置
[3, 4, 5, 8 | 6] ——> [3, 4, 5, 6, 8]
再拿6和5比较,6比5大,所以不需要交换位置
此时,未排序区间不存在元素,排序结束
用swift实现代码:
func insertionSort(_ array: inout [Int]) {
for x in 1..<array.count {
var y = x
while y > 0 && array[y] < array[y - 1] {
array.swapAt(y - 1, y)
y -= 1
}
}
}
// 调用
var array = [11,2,3,5,4,33,7,11,1]
insertionSort(&array)
print(array) // 输出:[1, 2, 3, 4, 5, 7, 11, 11, 33]
复杂类型的排序:
上面是int数组类型的排序,如果要在swift中给复杂类型排序,比如一个类,那就需要数组支持泛型了:
/// 支持泛型
/// - Parameters:
/// - array: 要排序的数组
/// - isOrderedBefore: 比较方法
func insertionSort<T>(_ array: inout [T], _ isOrderedBefore: (T, T) -> Bool) {
for x in 1..<array.count {
var y = x
while y > 0 && isOrderedBefore(array[y], array[y - 1]) {
array.swapAt(y - 1, y)
y -= 1
}
}
}
var numbers = [ 10, -1, 3, 9, 2, 27, 8, 5, 1, 3, 0, 26 ]
insertionSort(&numbers, <)
print(numbers) // 输出:[-1, 0, 1, 2, 3, 3, 5, 8, 9, 10, 26, 27]
insertionSort(&numbers, >)
print(numbers) // 输出:[27, 26, 10, 9, 8, 5, 3, 3, 2, 1, 0, -1]
上述代码,传入了一个返回值为Bool的方法isOrderedBefore,用于比较自定义类型的大小; < 和 > 决定排序顺序,分别是从小到大和从大到小
如果是更复杂的类型,可以这样:
var objects = [ obj1, obj2, obj3, ... ]
insertionSort(&objects) { $0.priority < $1.priority }
闭包是告诉 insertionSort() 根据对象的属性 priority 进行排序。
插入排序复杂度
- 最坏,平均时间复杂度:O(n^2)
- 最好时间复杂度:O(n)
- 空间复杂度:O(1)
- 当逆序对的数量极少时,插入排序的效率特别高。甚至速度比O(nlogn)级别的快速排序还要快。
- 数据量不是特别大的时候,插入排序的效率也是非常好的
插入排序的优化(一)
上面的插入排序核心思想是将未排序区间元素根据已排序区间元素,依次比较大小然后移动到合适的位置; 如果已排序区间元素比较大然后每次都需要交换元素,
如果能删除交换方法 swapAt() 会运行的更快
[ 3, 5, 8, 4 | 6 ]
<-->
swap
[ 3, 5, 4, 8 | 6 ]
<-->
swap
我们可以不交换,将数字向右移动,然后把新数字放到合适的位置就可以了。
// 该轮比较元素是4, 将4复制
[ 3, 5, 8, 4 | 6 ] 复制 4
*
[ 3, 5, 8, 8 | 6 ] 将 8 向右移动
--->
[ 3, 5, 5, 8 | 6 ] 将 5 向右移动
--->
[ 3, 4, 5, 8 | 6 ] 把 4 粘贴到合适的位置
*
用swift代码实现:
func insertionSort4(_ array:inout [Int]) {
for x in 1..<array.count {
var y = x
let temp = array[y]
while y > 0 && temp < array[y - 1] {
array[y] = array[y - 1]
y -= 1
}
array[y] = temp
}
}
var array = [11,2,3,5,4,33,7,11,1]
insertionSort4(&array)
print(array) // 输出:[1, 2, 3, 4, 5, 7, 11, 11, 33]
插入排序的优化(二)
插入排序的第二种优化方式可以采用二分搜索法(也叫做二分查找法)去已排序区间中查找并比较元素;
二分搜索法的实现原理举个例子: [1, 3, 8, 9, 20, 22, 23, 30, 35] 要查找30的索引:
- 先查找数组中的中位元素
20, 发现20比30小, 则去20的右边区间的中位元素继续查找 - 20到35的区间的中位元素是23, 查找到23,发现23比30
小, 继续向23的右边区间的中位元素查找 - 23到35的中位元素是30,查找结束!
二分搜索法在已排序数组中查找某个元素,效率非常高,因此也可用于插入排序上!
/// 利用二分查找法找出array中小于value的索引(数组从小到大排列)
/// - Parameters:
/// - array: 数组
/// - value: value
func searchIndex(array: [Int], value: Int) -> Int {
// 假设在数组[begin, end]范围中搜索某个元素v; mid = (begin+end)/2
// 如果v>value, 去[begin, mid]范围内二分搜索
// 如果v<=m, 去[mid+1, end]范围内二分搜索
// 当begin==end,退出
var begin: Int = 0;
var end: Int = array.count;
while begin < end {
let mid = (begin + end) >> 1; // 右移一位,即中分
if array[mid] > value {
end = mid;
}
else {
begin = mid + 1;
}
}
return begin;
}
归并排序(Merge Sort)
归并排序主要是用到了分治法的思想, 不断的将当前序列平均分割成子序列,直到不能分割;然后不断的将2个子序列合并成一个有序序列,直到最终只剩下一个有序序列,这就叫做归并排序。 归并排序其实就是拆分+合并
假定需要排序的数组为:[8, 7, 6, 5, 4, 3, 2, 1],按照从小到大排序,其排序路径如下:
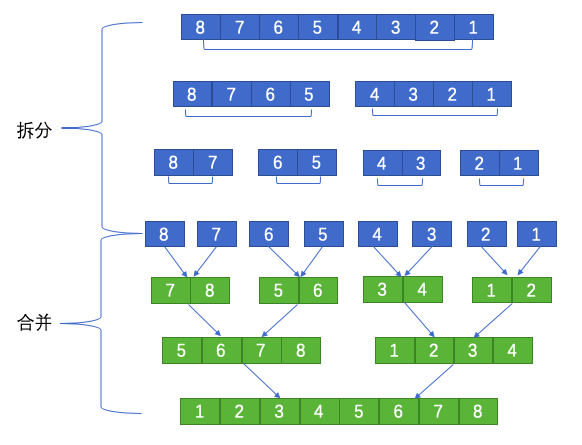
拆分逻辑
拆分并不复杂,只需遍历数组,然后装入新数组中即可,其大概实现如下:
/// 拆分数组
/// - Parameter items: 新数组
func divideArray(items: Array<Int>) -> Array<Array<Int>> {
var tempArray: Array<Array<Int>> = []
for item in items {
var subArray: Array<Int> = []
subArray.append(item)
tempArray.append(subArray)
}
return tempArray
}
合并逻辑
合并(两两合并)有点复杂,其实现逻辑如下:
- 两个数组都有一个指向
头节点的指针。 - 比较两个指针对应值的大小,将小的值取出,并将其指针向后移动一位。
完整代码:
/// 使用归并数组将两个有序数组合并
/// - Parameters:
/// - firstList: 第一个有序数组
/// - secondList: 第二个有序数组
func mergeArray(firstList: Array<Int>, secondList: Array<Int>) -> Array<Int> {
var resultList: Array<Int> = []
var firstIndex = 0
var secondIndex = 0
while firstIndex < firstList.count && secondIndex < secondList.count {
if firstList[firstIndex] < secondList[secondIndex] {
resultList.append(firstList[firstIndex])
firstIndex += 1
}
else {
resultList.append(secondList[secondIndex])
secondIndex += 1
}
}
while firstIndex < firstList.count {
resultList.append(firstList[firstIndex])
firstIndex += 1
}
while secondIndex < secondList.count {
resultList.append(secondList[secondIndex])
secondIndex += 1
}
return resultList;
}
func sort(items: Array<Int>) -> Array<Int> {
// 将数组中的每一个元素放入一个新数组中
var tempArray: Array<Array<Int>> = []
for item in items {
var subArray: Array<Int> = []
subArray.append(item)
tempArray.append(subArray)
}
// 对这个数组中的数组进行合并,直到合并完毕为止
while tempArray.count != 1 {
print(tempArray)
var i = 0
while i < tempArray.count - 1 {
print("将\(tempArray[i])与\(tempArray[i+1])进行合并\n")
tempArray[i] = mergeArray(firstList: tempArray[i], secondList: tempArray[i+1])
print("合并结果:\(tempArray[i])\n")
tempArray.remove(at: i+1)
i = i+1
}
}
return tempArray.first!
}
let arrays = [1,3,4,52,1,4234,113,2]
print(sort(items: arrays))
通过上述日志输出,我们可以很清晰的看到拆分和合并的整个过程:

- 由于归并排序总是平均分割子序列,所以最好,最坏,平均时间复杂度都是O(nlogn),属于稳定排序。 归并排序的空间复杂度是O(n)
- 归并排序的空间复杂度是O(n)
快速排序(Quicksort)
快速排序算法是通过多次比较和交换来实现排序的,其排序流程如下:
- 首先设定一个分界值,通过该分界值将数组分成左右两部分
- 将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于分界值,而右边部分中各元素都大于或等于分界值
- 然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理
- 重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了
swift:
func quickSort(a: inout [Int], low: Int, high: Int) {
if low >= high { // 递归结束条件
return
}
var i = low
var j = high
let key = a[i]
while i < j {
// 从右边开始比较,比key大的数位置不变
while i < j && a[j] >= key {
j -= 1
}
// 只要出现一个比key小的数,将这个数放入左边i的位置
a[i] = a[j]
// 从左边开始比较,比key小的数位置不变
while i < j && a[i] <= key {
i += 1
}
// 只要出现一个比key大的数,将这个数放入右边j的位置
a[j] = a[i]
}
a[i] = key // 将key放入i的位置,则左侧数都比key小,右侧数都比key大
quickSort(a: &a, low: low, high: i - 1) // 左递归
quickSort(a: &a, low: i + 1, high: high) // 右递归
}
// 示例
var m = [2,3,5,7,1,4,6,15,5,2,7,9,10,15,9,17,12]
quickSort(a: &m, low: 0, high: m.count - 1)
print(m)
// 结果:[1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 9, 9, 10, 12, 15, 15, 17]
OC:
+ (void)quickSort:(NSMutableArray *)m low:(int)low high:(int)high{
if (low >= high) {
return;
}
int i = low;
int j = high;
id key = m[i];
while (i<j) {
while (i<j && [m[j] intValue] >= [key intValue]) {
j--;
}
if (i == j) { // 当key是目前最小的数时,会出现i=j的情况,
break;
}
m[i++] = m[j]; // i++ 会减少一次m[i]和key的比较
while (i < j && [m[i] intValue] <= [key intValue]) {
i++;
}
if (i == j) { // 当key是目前最大的数时(m[j]的前面),会出现i=j的情况
break;
}
m[j--] = m[i]; //j-- 会减少一次m[j]和key的比较
}
m[i] = key;
[self quickSort: m low: low high: i-1];
[self quickSort: m low: i+1 high: high];
// NSLog(@"快速排序 %@",m);
本文首次发布于 孙忠良 Blog, 作者 [@sunzhongliang] , 转载请保留原文链接.