数据结构是计算机存储、组织数据的方式
本文演示代码为Swift语言
树(Tree)

树又分为以下几种:
- 有序树
- 树中任意节点的子节点之间有顺序关系
- 无序树
- 树中任意节点的子节点之间没有顺序关系(也叫做
自由树)
- 树中任意节点的子节点之间没有顺序关系(也叫做
- 森林
- 由m(m >= 0)棵互不相交的数组成的集合
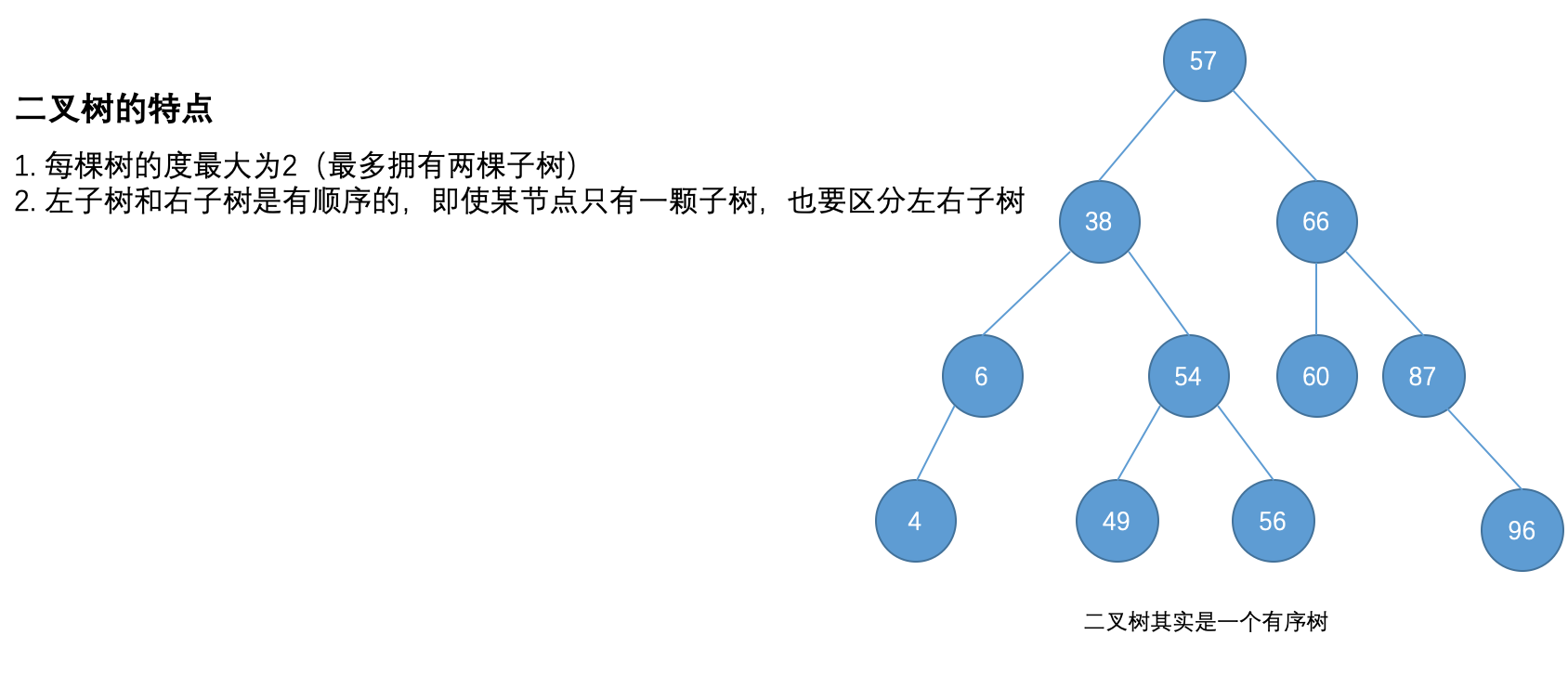
二叉树(Binary Tree)
真二叉树(Proper Binary Tree)
真二叉树:所有节点的度要么为0,要么为2
满二叉树(Full Binary Tree)
满二叉树:所有节点的度要么为0,要么为2,且所有的叶子节点都在最后一层
在同样高度的二叉树中,满二叉树的叶子节点数量最多,总节点数量最多
满二叉树一定是真二叉树,真二叉树不一定是满二叉树
完全二叉树(Complete Binary Tree)
完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树),第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
其实是:叶子节点只会出现的最后两层,且最后一层的叶子节点都靠左对齐
完全二叉树从根节点至倒数第二层是一棵满二叉树
满二叉树一定是一棵完全二叉树,完全二叉树不一定是满二叉树
二叉搜索树(Binary Search Tree)
二叉搜索树是二叉树的一种,是应用非常广泛的一种二叉树,英文简称BST,它又被称为二叉查找树、二叉排序树,其有以下特点:
1.任意一个节点的值都大于其左子树所有节点的值
2.任意一个节点的值都小于其右子树所有的值
3.它的左右子树也是一棵二叉搜索树
总结来说就是:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
二叉搜索树存储的元素必须具备可比较性,比如int、double等,但如果是自定义类型,需要指定比较方式
比如swift当中自定义类型就需要实现Equatable协议
不允许存储null值
思考下面一道练习题
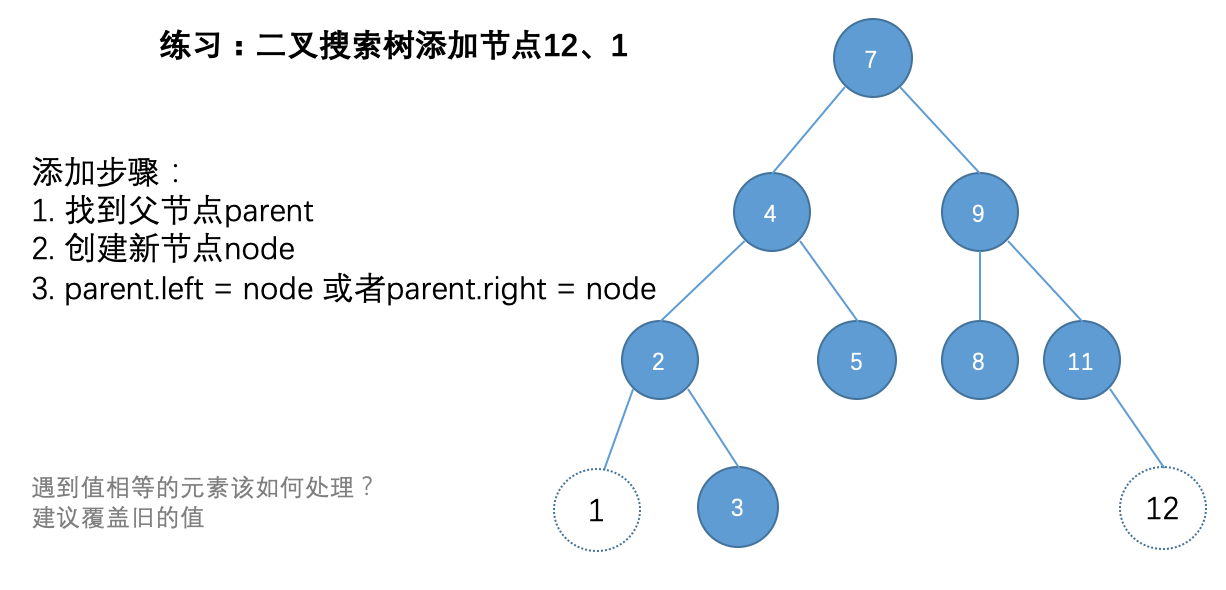
比如向二叉搜索树中添加节点12,程序当中应该这样实现:
- 用变量node指向二叉搜索树的
parent - 声明变量tmpParent用于保存当前循环到哪棵树上
while循环(node!=null)遍历整个二叉树- 将当前正在遍历的节点赋值给tmpParent
- 如果要添加的节点值
大于当前遍历的节点值- node = node.right(说明遍历到这个节点了,赋值给node了,继续遍历)
- 如果要添加的节点值
小于当前遍历的节点值- node = node.left(说明遍历到这个节点了,赋值给node了,继续遍历)
- 否则(相等情况)
- return
- 创建新节点newNode(element=要添加的节点值, parent=上面while循环获取的tmpParent)
- 如果节点值
大于tmpParent的节点值- 往tmpParent的右节点添加创建的节点
- 如果节点值
小于tmpParent的节点值- 往tmpParent的左节点添加创建的节点
以上的代码逻辑,就能满足二叉树的添加操作了
二叉搜索树接口设计
// 元素的数量
int size();
// 是否为空
Bool isEmpty();
// 清空所有元素
void clear();
// 添加元素
void add(T element)
// 删除元素
void remove(T element)
// 是否包含某元素
Bool contains(T element)
二叉搜索树实现
// 本文示例为了简单,以Int类型。实际工作场景应当是支持泛型的
// 本文示例为了简单,以Int类型
class BinarySearchTree {
private var size: Int = 0
private var root: Node? = nil
func getSize() -> Int {
return self.size
}
func isEmpty() -> Bool {
return self.size == 0
}
func clear() {
self.root = nil
self.size = 0
}
func add(element: Int) {
// 添加的是根节点
if self.root == nil {
self.root = BinarySearchTree.Node(element: element, parent: nil)
self.size = self.size + 1
return
}
// 使用临时变量保存要添加的父节点
var tmpParent: Node? = nil
// 找到父节点
var node = root
while node != nil {
// 将当前遍历的节点赋值给tmpParent
tmpParent = node
// 比较新添加的元素是否 大于 根节点的值
if element > node!.element {
node = node!.right
}
else if element < node!.element { // 小于
node = node!.left
}
else { // 相等
return
}
}
let newNode = BinarySearchTree.Node(element: element, parent: tmpParent);
if element > tmpParent!.element {
tmpParent?.right = newNode
}
else {
tmpParent?.left = newNode
}
self.size = self.size + 1
}
/// 删除节点值
/// - Parameter element: 节点值
func remove(element: Int) {
var node = self.node(element: element)
removeNode(node: &node);
}
func contains(element: Int) -> Bool {
return false
}
/// 删除节点
/// - Parameter node: 节点
private func removeNode(node: inout Node?) {
if node == nil {
return
}
self.size = self.size - 1
if node?.left != nil && node?.right != nil { // 度为2的节点
// 找到后继节点
let s = self.successor(node: &node)
// 用后继节点的值覆盖度为2的节点的值
node?.element = s!.element
// 删除后继节点
node = s
}
// 删除node节点(node的度必然是1或者0)
let replacement = node?.left != nil ? node?.left : node?.right
if replacement != nil { // node是度为1的节点
replacement?.parent = node?.parent // 更改parent
// 更改parent的left、right的指向
if node?.parent == nil { // node是度为1的节点并且是根节点
root = replacement
}
else if node == node?.parent?.left {
node?.parent?.left = replacement
}
else {
node?.parent?.right = replacement
}
}
else if node?.parent == nil { // node是叶子节点并且是根节点
root = nil
}
else { // node是叶子节点,但不是根节点
if node == node?.parent?.left {
node?.parent?.left = nil
}
else { // node == node.parent.right
node?.parent?.right = nil
}
}
}
/// 后继节点
/// - Parameter node: 要查找的节点
private func successor(node: inout Node?) -> Node? {
if node == nil {
return nil
}
// 前驱节点在左子树当中(right.left.left.left....)
var p = node?.right
if (p != nil) {
while (p!.left != nil) {
p = p!.left;
}
return p;
}
// 从父节点、祖父节点中寻找前驱节点
while (node!.parent != nil && node == node!.parent!.right) {
node = node!.parent;
}
return node!.parent;
}
/// 根据节点值查找node
/// - Parameter element: 节点值
private func node(element: Int) -> Node? {
var node = root
while node != nil {
if element == node!.element {
return node
}
if element > node!.element {
node = node?.right
}
else {
node = node?.left
}
}
return nil
}
class Node: Equatable {
static func == (lhs: BinarySearchTree.Node, rhs: BinarySearchTree.Node) -> Bool {
return lhs.element == rhs.element
}
var element: Int
// 左子节点
var left: Node? = nil
// 右子节点
var right: Node? = nil
// 父子节点
var parent: Node?
init(element: Int, parent: Node?) {
self.element = element
self.parent = parent
}
}
// 前序遍历
func preOrderTraversal() {
self._preOrderTraversal(node: self.root)
}
// 中序遍历
func preInOrderTraversal() {
self._preInOrderTraversal(node: self.root)
}
// 后序遍历
func postOrderTraversal() {
self._postOrderTraversal(node: self.root)
}
// 层序遍历
func levelOrderTraversal() {
self._levelOrderTraversal(node: self.root)
}
// 计算二叉树的高度
func getTreeHeight() -> Int {
return _getTreeHeight(node: self.root)
}
// 计算二叉树的高度
func getTreeHeight_Order() -> Int {
if self.root == nil {
return 0
}
// 声明一个队列(使用的是之前数据结构创建的Queue)
let queue = Queue<Node?>()
// 将树的根节点入队
queue.enQueue(element: self.root)
// 树的总高度
var height = 0
// 当前这一层节点的个数(初始化为1:根节点的高度)
var levelSize = queue.size
while !queue.isEmpty() {
let node = queue.deQueue() // 出队
levelSize = levelSize - 1 // 当前这一层未访问节点的个数-1
if node?.left != nil {
queue.enQueue(element: node?.left)
}
if node?.right != nil {
queue.enQueue(element: node?.right)
}
if levelSize == 0 { // 减到0了,说明即将要访问下一层
levelSize = queue.size // 这时候队列里存放的是下一全部子节点
height = height + 1 // 总高度+1
}
}
return height
}
// 判断二叉树是否是完全二叉树
func isCompleteTree() -> Bool {
if self.root == nil {
return false
}
// 声明队列
let queue = Queue<Node?>();
// 将树的根节点入队
queue.enQueue(element: self.root)
var leaf = false
while !queue.isEmpty() {
// 出队
let node = queue.deQueue();
// 是否是叶子节点(节点的左右都为空)
let isLeaf = node?.left == nil && node?.right == nil
if leaf && !isLeaf {
return false
}
if node?.left != nil && node?.right != nil {
// 左右节点都有值(入队)
queue.enQueue(element: node?.left)
queue.enQueue(element: node?.right)
}
else if (node?.left == nil && node?.right != nil) {
// 左节点为空,右节点不为空,直接判定是非完全二叉树
return false
}
else { // 后面遍历的节点都必须是叶子节点
leaf = true
}
}
return true
}
// 二叉树翻转(中序遍历)
func invertTree(root: Node?) -> Node? {
if root == nil {
return root
}
let queue = Queue<Node?>()
queue.enQueue(element: self.root)
while !queue.isEmpty() {
let node = queue.deQueue()
let tmp = root?.left
root?.left = root?.right
root?.right = tmp
if node?.left != nil {
queue.enQueue(element: node?.left)
}
if node?.right != nil {
queue.enQueue(element: node?.right)
}
}
return root
}
//----私有实现方法----前序遍历
private func _preOrderTraversal(node: Node?) {
if node == nil {
return
}
print("节点为:\(node?.element ?? -1)")
_preOrderTraversal(node: node?.left)
_preOrderTraversal(node: node?.right)
}
//----私有实现方法----中序遍历
private func _preInOrderTraversal(node: Node?) {
if node == nil {
return
}
_preInOrderTraversal(node: node?.left)
print("节点为\(node?.element ?? -1)")
_preInOrderTraversal(node: node?.right)
}
//----私有实现方法----后序遍历
private func _postOrderTraversal(node: Node?) {
if node == nil {
return
}
_postOrderTraversal(node: node?.left)
_postOrderTraversal(node: node?.right)
print("节点为\(node?.element ?? -1)")
}
//----私有实现方法----层序遍历
private func _levelOrderTraversal(node: Node?) {
if root == nil {
return
}
let queue = Queue<Node?>()
queue.enQueue(element: root)
while !queue.isEmpty() {
let node = queue.deQueue()
print("节点为\(node?.element ?? -1)")
if node?.left != nil {
queue.enQueue(element: node?.left)
}
if node?.right != nil {
queue.enQueue(element: node?.right)
}
}
}
//----私有实现方法----获取二叉树的高度
private func _getTreeHeight(node: Node?) -> Int {
if node == nil {
return 0
}
let leftHeight = _getTreeHeight(node: node?.left)
let rightHeight = _getTreeHeight(node: node?.right)
return 1 + (leftHeight >= rightHeight ? leftHeight : rightHeight)
}
}
测试代码:
let bst = BinarySearchTree();
bst.add(element: 7)
bst.add(element: 4)
bst.add(element: 9)
bst.add(element: 2)
bst.add(element: 5)
bst.add(element: 8)
bst.add(element: 11)
bst.add(element: 3)
print(bst.getSize())
二叉树的遍历
遍历是数据结构中的常见操作,一般是指将所有元素都访问一遍的操作
线性数据结构的遍历比较简单
1.正序遍历
2.逆序遍历
但根据节点访问顺序的不同,二叉树的常见遍历方式有4种
1.前序遍历(Preorder Traversal)
2.中序遍历(Inorder Traversal)
3.后续遍历(Postorder Traversal)
4.层序遍历(Level Order Traversal)
前序遍历
前序遍历指的是先访问根节点, 再前序遍历左子树,前序遍历右子树
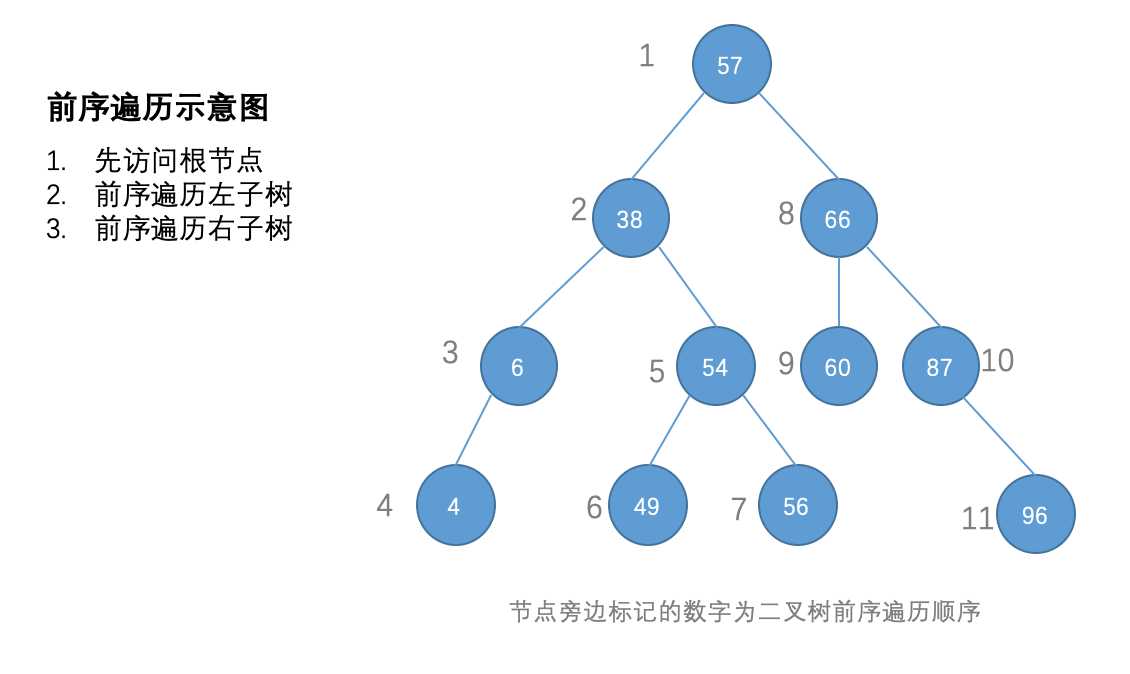 实现代码:
实现代码:
// 前序遍历
func preOrderTraversal() {
self._preOrderTraversal(node: self.root)
}
private func _preOrderTraversal(node: Node?) {
if node == nil {
return
}
print("节点为:\(node?.element ?? -1)")
_preOrderTraversal(node: node?.left)
_preOrderTraversal(node: node?.right)
}
测试代码:
let bst = BinarySearchTree();
bst.add(element: 7)
bst.add(element: 4)
bst.add(element: 2)
bst.add(element: 9)
bst.add(element: 5)
bst.add(element: 1)
bst.add(element: 8)
bst.add(element: 11)
bst.add(element: 12)
bst.add(element: 3)
// 前序遍历
bst.preOrderTraversal()
// -------
// 控制台输出:7、4、2、1、3、5、9、8、11、12
中序遍历
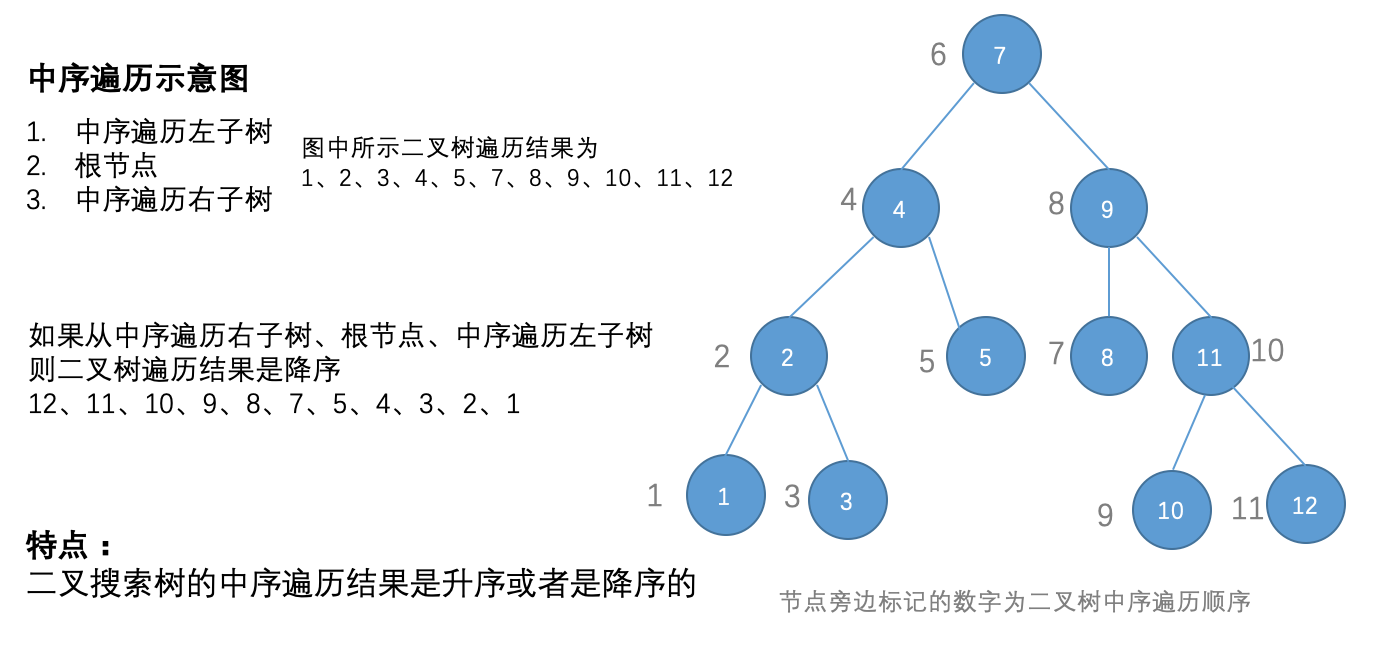 实现代码:
实现代码:
// 中序遍历
func preInOrderTraversal() {
self._preInOrderTraversal(node: self.root)
}
//----私有实现方法----中序遍历
private func _preInOrderTraversal(node: Node?) {
if node == nil {
return
}
_preInOrderTraversal(node: node?.left)
print("节点为\(node?.element ?? -1)")
_preInOrderTraversal(node: node?.right)
}
测试代码:
let bst = BinarySearchTree();
bst.add(element: 7)
bst.add(element: 4)
bst.add(element: 2)
bst.add(element: 9)
bst.add(element: 5)
bst.add(element: 1)
bst.add(element: 8)
bst.add(element: 11)
bst.add(element: 12)
bst.add(element: 3)
// 中序遍历
bst.preInOrderTraversal()
// 输出1、2、3、4、5、7、8、9、11、12
后序遍历
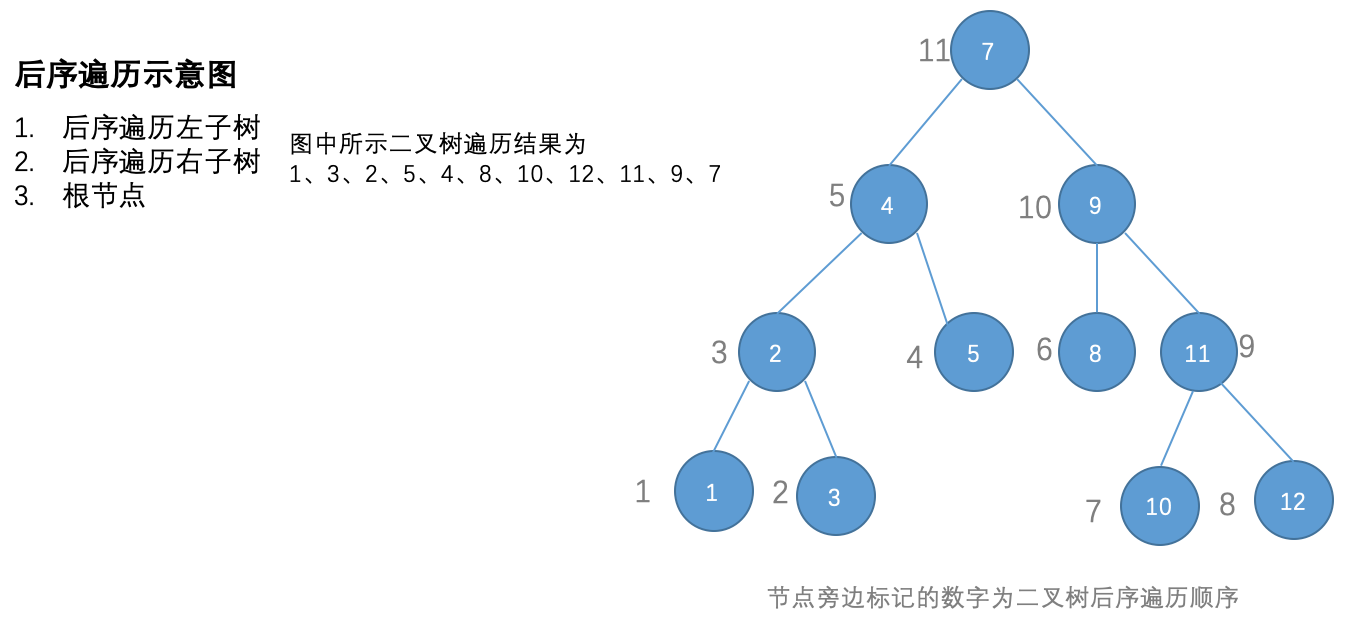 实现代码:
实现代码:
// 后序遍历
func postOrderTraversal() {
self._postOrderTraversal(node: self.root)
}
//----私有实现方法----后序遍历
private func _postOrderTraversal(node: Node?) {
if node == nil {
return
}
_postOrderTraversal(node: node?.left)
_postOrderTraversal(node: node?.right)
print("节点为\(node?.element ?? -1)")
}
测试代码:
let bst = BinarySearchTree();
bst.add(element: 7)
bst.add(element: 4)
bst.add(element: 2)
bst.add(element: 9)
bst.add(element: 5)
bst.add(element: 1)
bst.add(element: 8)
bst.add(element: 11)
bst.add(element: 12)
bst.add(element: 3)
// 后序遍历
bst.postOrderTraversal()
// 输出1、3、2、5、4、8、12、11、9、7
层序遍历
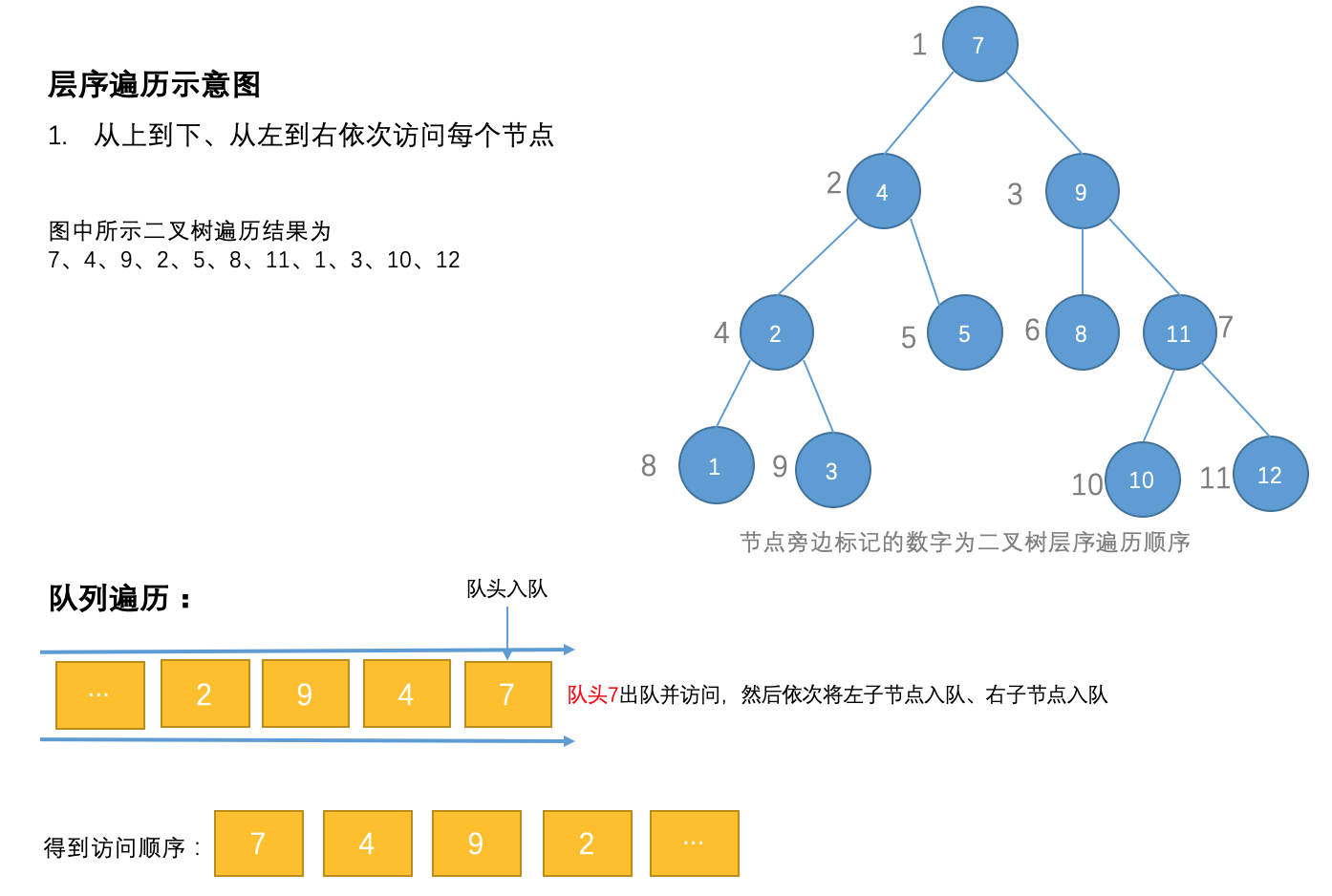 对于
对于层序遍历来说,由于遍历的顺序是从上到下,从左到右依次遍历,递归操作是无法满足要求的,此时可选择使用队列来实现:
- 将根节点入队
- 循环执行以下操作,直到队列为空
- 将队列头节点
A出队,进行访问 - 将
A的左子节点入队 - 将
A的右子节点入队
- 将队列头节点
实现代码:
// 层序遍历
func levelOrderTraversal() {
self._levelOrderTraversal(node: self.root)
}
//----私有实现方法----层序遍历
private func _levelOrderTraversal(node: Node?) {
if root == nil {
return
}
// 这里的队列使用的是前面文章所实现的队列
let queue = Queue<Node?>()
queue.enQueue(element: root)
while !queue.isEmpty() {
let node = queue.deQueue()
print("节点为\(node?.element ?? -1)")
if node?.left != nil {
queue.enQueue(element: node?.left)
}
if node?.right != nil {
queue.enQueue(element: node?.right)
}
}
}
代码测试:
let bst = BinarySearchTree();
bst.add(element: 7)
bst.add(element: 4)
bst.add(element: 2)
bst.add(element: 9)
bst.add(element: 5)
bst.add(element: 1)
bst.add(element: 8)
bst.add(element: 11)
bst.add(element: 12)
bst.add(element: 3)
// 层序遍历
bst.levelOrderTraversal()
// 输出7、4、9、2、5、8、11、1、3、12
算法练习
计算二叉树的高度
题目:给出一个二叉树,计算出来它的高度
题解:
计算二叉树的高度,其本质上是算出根节点到所有叶子节点的最远距离, 可以使用递归和迭代计算
递归法:
// 计算二叉树的高度
func getTreeHeight() -> Int {
return _getTreeHeight(node: self.root)
}
//----私有实现方法----计算二叉树的高度
private func _getTreeHeight(node: Node?) -> Int {
if node == nil {
return 0
}
let leftHeight = _getTreeHeight(node: node?.left)
let rightHeight = _getTreeHeight(node: node?.right)
return 1 + (leftHeight >= rightHeight ? leftHeight : rightHeight)
}
代码测试:
let bst = BinarySearchTree();
bst.add(element: 7)
bst.add(element: 4)
bst.add(element: 2)
bst.add(element: 9)
bst.add(element: 5)
bst.add(element: 1)
bst.add(element: 8)
bst.add(element: 11)
bst.add(element: 12)
bst.add(element: 3)
print("二叉树的高度:\(bst.getTreeHeight())") // 输出4
迭代法:
// 计算二叉树的高度
func getTreeHeight_Order() -> Int {
if self.root == nil {
return 0
}
// 声明一个队列(使用的是之前数据结构创建的Queue)
let queue = Queue<Node?>()
// 将树的根节点入队
queue.enQueue(element: self.root)
// 树的总高度
var height = 0
// 当前这一层节点的个数(初始化为1:根节点的高度)
var levelSize = queue.size
while !queue.isEmpty() {
let node = queue.deQueue() // 出队
levelSize = levelSize - 1 // 当前这一层未访问节点的个数-1
// 判断节点的左右节点,如果不为空,就将节点添加到队列尾端
if node?.left != nil {
queue.enQueue(element: node?.left)
}
if node?.right != nil {
queue.enQueue(element: node?.right)
}
if levelSize == 0 { // 减到0了,说明即将要访问下一层
levelSize = queue.size // 这时候队列里存放的是下一全部子节点
height = height + 1 // 总高度+1
}
}
return height
}
感觉队列是一种微妙的数据结构,有时候用来解决一些问题还是非常有用处的
判断一棵树是否为完全二叉树
题目:判断一棵树是否为完全二叉树
完全二叉树:是从上到下、从左到右依次排列这一棵树,叶子节点只会出现的最后两层,且最后一层的叶子节点都靠左对齐
题解:
因为完全二叉树的特点(从上到下、从左到右依次排列,叶子节点靠左对齐), 利用层序遍历法来实现是比较简单的
// 判断二叉树是否是完全二叉树
func isCompleteTree() -> Bool {
if self.root == nil {
return false
}
// 声明队列
let queue = Queue<Node?>();
// 将树的根节点入队
queue.enQueue(element: self.root)
var leaf = false
while !queue.isEmpty() {
// 出队
let node = queue.deQueue();
// 是否是叶子节点(节点的左右都为空)
let isLeaf = node?.left == nil && node?.right == nil
if leaf && !isLeaf {
return false
}
if node?.left != nil && node?.right != nil {
// 左右节点都有值(入队)
queue.enQueue(element: node?.left)
queue.enQueue(element: node?.right)
}
else if (node?.left == nil && node?.right != nil) {
// 左节点为空,右节点不为空,直接判定是非完全二叉树
return false
}
else { // 后面遍历的节点都必须是叶子节点
leaf = true
}
}
return true
}
代码测试:
let bst = BinarySearchTree();
bst.add(element: 7)
bst.add(element: 4)
bst.add(element: 2)
bst.add(element: 9)
bst.add(element: 5)
bst.add(element: 1)
bst.add(element: 8)
bst.add(element: 11)
bst.add(element: 12)
bst.add(element: 3)
print("完全二叉树:\(bst.isCompleteTree())") // false
let bst1 = BinarySearchTree();
bst1.add(element: 7)
bst1.add(element: 4)
bst1.add(element: 9)
bst1.add(element: 2)
bst1.add(element: 2)
print("完全二叉树:\(bst1.isCompleteTree())") // true
翻转二叉树

这道题是
Homebrew的作者Max Howell去谷歌面试时,被问到的一个问题,结果作者都没能在白板上写出答案😂
Google:90% of our engineers use the software you wrote(Homebrew), but you can’t invert a binary tree on a whiteboard so fuck off.
题解:
翻转其实是将所有节点的左右子树进行交换, 其实如果会遍历二叉树,那么这道题就很好做了
前序遍历翻转法:
// 二叉树翻转(前序遍历)
func invertTree(root: Node?) -> Node? {
if root == nil {
return root
}
let tmp = root?.left
root?.left = root?.right
root?.right = tmp
invertTree(root: root?.left)
invertTree(root: root?.right)
return root
}
中序遍历翻转法:
// 二叉树翻转(中序遍历)
func invertTree(root: Node?) -> Node? {
if root == nil {
return root
}
invertTree(root: root?.left)
let tmp = root?.left
root?.left = root?.right
root?.right = tmp
invertTree(root: root?.left) // 这里要注意:必须要left,因为right已经交换过了
return root
}
层序遍历翻转法:
// 二叉树翻转(层序遍历)
func invertTree(root: Node?) -> Node? {
if root == nil {
return root
}
let queue = Queue<Node?>()
queue.enQueue(element: self.root)
while !queue.isEmpty() {
let node = queue.deQueue()
let tmp = node?.left
node?.left = node?.right
node?.right = tmp
if node?.left != nil {
queue.enQueue(element: node?.left)
}
if node?.right != nil {
queue.enQueue(element: node?.right)
}
}
return root
}
前驱节点
前驱节点: 中序遍历时的前一个节点(如果是搜索二叉树,那么前驱节点就是前一个比它小的节点)
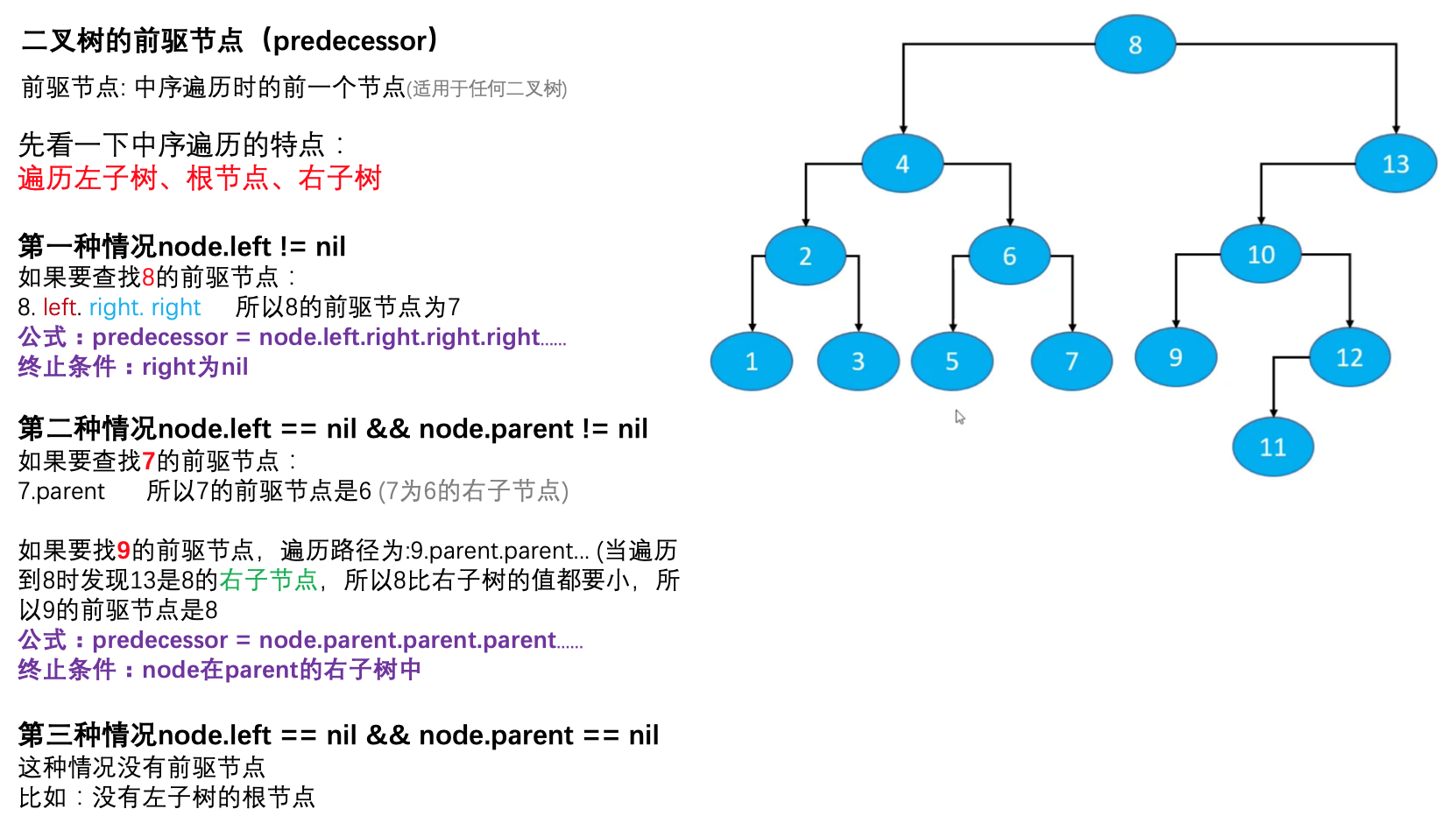
func predecessor(node: inout Node?) -> Node? {
if node == nil {
return nil
}
// 前驱节点在左子树当中(left.right.right.right...)
var p = node?.left;
if p != nil {
while p?.right != nil {
p = p?.right
}
return p
}
// 从父节点开始寻找 前驱节点
while node?.parent != nil && node?.parent?.left == node {
node = node?.parent
}
return node?.parent
}
后继节点
后继节点和前驱节点是反着的,即:中序遍历时的后一个节点(如果是搜索二叉树,那么后继节点就是后一个比他大的节点)
/// 后继节点
/// - Parameter node: 要查找的节点
private func successor(node: inout Node?) -> Node? {
if node == nil {
return nil
}
// 前驱节点在左子树当中(right.left.left.left....)
var p = node?.right
if (p != nil) {
while (p!.left != nil) {
p = p!.left;
}
return p;
}
// 从父节点、祖父节点中寻找前驱节点
while (node!.parent != nil && node == node!.parent!.right) {
node = node!.parent;
}
return node!.parent;
}
本文首次发布于 孙忠良 Blog, 作者 [@sunzhongliang] , 转载请保留原文链接.