数据结构-队列

数据结构是计算机存储、组织数据的方式
本文演示代码为Swift语言

队列(Queue)

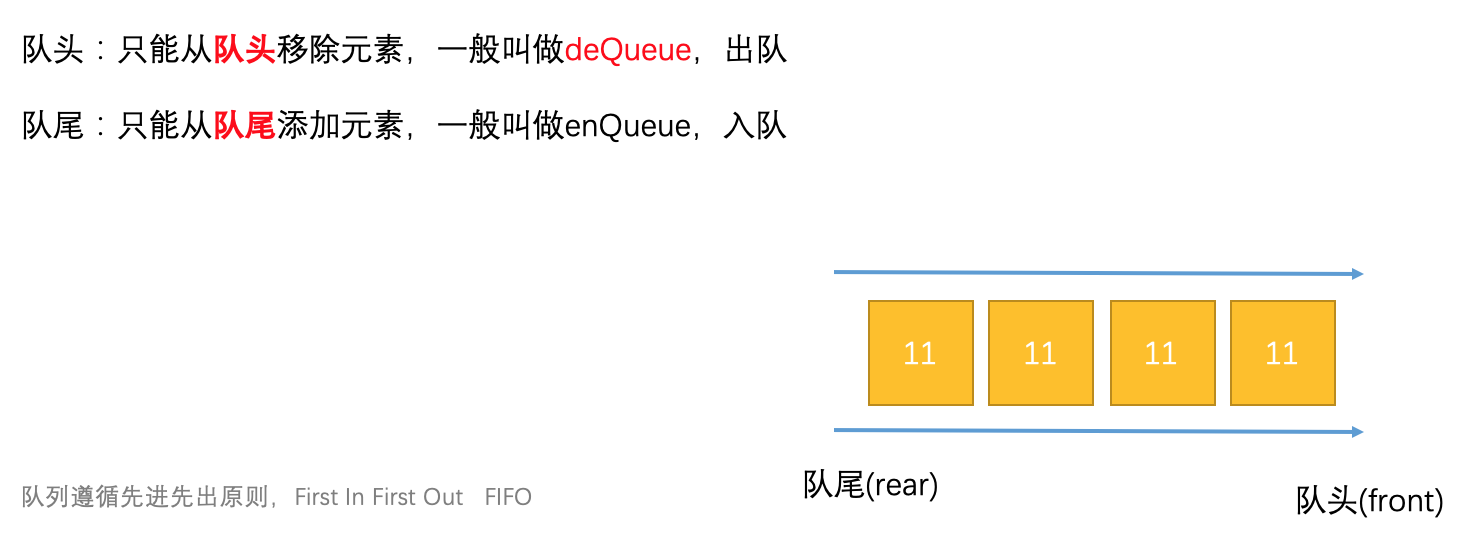
队列是一种特殊的线性表，只能在数据的头尾两端进行操作

队列的接口设计

/*
* 方法
*/
// 元素的数量
int size()
// 是否为空
Bool isEmpty()
// 入队
void enQueue(T element)
// 出队
T deQueue()
// 获取队列的头元素
T front()
// 清空队列
void clear()

队列可以选择使用动态数组或者链表来实现，但因为队列主要是往头尾两端操作元素，所以使用双向链表来实现比较好

队列实现

class Queue<T> {
    var size: Int = 0
    var firstNode: Node<T>? = nil
    var lastNode: Node<T>? = nil
    
    class Node<T> {
        var element: T
        var nextNode: Node<T>?
        var prevNode: Node<T>?
        
        init(prevNode: Node<T>?, element: T, nextNode: Node<T>?) {
            self.prevNode = prevNode
            self.element = element
            self.nextNode = nextNode
        }
    }
    
    /// 清空队列
    func clear() {
        self.size = 0
        self.firstNode = nil
        self.lastNode = nil
    }
    
    // 是否为空
    func isEmpty() -> Bool {
        return self.size == 0
    }
    
    // 获取队首元素
    func front() -> T {
        return self.get(index: 0).element
    }
    
    // 入队
    func enQueue(element: T) {
        self.add(element: element)
    }
    
    // 出队
    func deQueue() -> T {
        return self.remove(index: 0)
    }
    
    /// 删除index位置的节点
    ///
    /// - Parameter index: index
    /// - Returns: 删除的节点
    private func remove(index: Int) -> T {
        let node = self.node(index: index)
        let prev = node.prevNode
        let next = node.nextNode
        
        // 首节点删除
        if prev == nil {
            self.firstNode = next
        }
        else {
            prev?.nextNode = next
        }
        
        // 尾节点删除
        if next == nil {
            self.lastNode = prev
        }
        else {
            next?.prevNode = prev
        }
        self.size = self.size - 1
        return node.element
    }
    
    /// 在index位置添加新节点
    ///
    /// - Parameters:
    ///   - index: index
    ///   - element: 节点
    private func add(index: Int, element: T) {
        // 往最后节点添加元素
        if index == self.size {
            let oldLast: Node<T>? = self.lastNode
            self.lastNode = Queue.Node(prevNode: oldLast, element: element, nextNode: nil)
            // 这是链表添加的第一个元素
            if oldLast == nil {
                self.firstNode = self.lastNode
            }
            else {
                oldLast?.nextNode = self.lastNode
            }
        }
        else {
            // 获取要添加节点
            let next = node(index: index);
            // 获取要添加节点的上一个节点
            let prev = next.prevNode;
            // 创建新节点
            let node = Queue.Node(prevNode: prev, element: element, nextNode: next)
            // 连线
            next.prevNode = node
            
            // 如果要添加的节点在首节点(首节点.prev == nil)
            if prev == nil {
                self.firstNode = node
            }
            else {
                prev?.nextNode = node
            }
        }
        
        // 总长度+1
        self.size = self.size + 1
    }
    
    private func add(element: T) {
        self.add(index: self.size, element: element)
    }
    
    /// 获取index位置的节点
    ///
    /// - Parameter index: index
    /// - Returns: 节点
    private func get(index: Int) -> Node<T> {
        return self.node(index: index)
    }
    
    /// 根据index查找node节点
    ///
    /// - Parameter index: 索引
    /// - Returns: node节点
    private func node(index: Int) -> Node<T> {
        if index > self.size {
            // TODO: 索引检查
        }
        
        // 如果要查找的index < 当前总长度的一半
        // 说明要查找的元素在链表的左侧(往后找)
        if index < self.size >> 1 {
            var node: Node<T>? = self.firstNode
            for _ in 0..<index {
                node = node!.nextNode
            }
            return node!
        }
        else { // 要查找的元素在链表的右侧(往前找)
            var node: Node<T>? = self.lastNode
            // 从self.size-1开始，到index结束，每次-1
            for _ in stride(from: self.size-2, through: index, by: -1) {
                node = node!.prevNode
            }
            return node!
        }
    }
    
    func toString() -> Void {
        var node: Node<T>? = self.firstNode
        for _ in 0..<self.size {
            print(node?.element ?? "")
            node = node?.nextNode
        }
    }
}

测试：

let que = Queue<String>()
que.enQueue(element: "1111")
que.enQueue(element: "2222")
que.enQueue(element: "3333")
que.enQueue(element: "4444")
que.toString() // 输出 1111、2222、3333、4444

que.deQueue()
print("出队后剩余:")
que.toString() // 输出2222、3333、4444

双端队列(Deque)

双端队列(double ended queue)是能够在头尾两端添加、删除元素的队列

/*
* 方法
*/

// 元素的数量
int size();
// 是否为空
Bool isEmpty();
// 清空
void clear();
// 从队尾入栈
void enQueueRear(T element)
// 从队头出队
T deQueueFront();
// 从队头入队
void enQueueFront(T element)
// 从队尾出队
T deQueueRear();
// 获取队列的头元素
T front();
// 获取队列的尾元素
T rear();

可以看得出双端队列其实就是比队列多了一种数据的操作方式(可以从队尾和对头入队、出队), 用双向链表来实现也比较简单，这里就不过多实现了

循环队列(Circle Queue)

循环队列：可以进行两端添加、删除操作的循环队列
循环队列底层是用动态数组来实现，其原理如下：
使用一个front指针来指向队列的队头，假设动态数组初始容量是10，初始化后依次向里面添加了10个元素，其front指针就指向0的位置，随后又删除了第0个元素, 那么front指针就会指向1的位置，再往里面添加数据时，就会利用front指针指向的位置来利用剩余的空间

优先级队列

普通队列是FIFO原则，也就是先进先出，但优先级队列则是按照优先级高低进行出队，比如将优先级最高的元素作为队头优先出队
在实际工作场景当中，也有很多地方会用到优先级队列的

优先级队列实现

优先级队列实现可采用二叉堆来实现

算法练习

用栈来实现普通队列

原文地址: 用栈实现队列

分析:
由于栈的特点是后进先出(Last In First Out)，但是队列是先进先出(Fist In First Out)，所以要想用栈来实现一个队列，可以考虑使用两个栈来实现
准备两个栈，命名为: inStack和outStack

入队时，push到inStack中
出队时
- 如果outStack为空，将inStack所有元素逐一弹出，push到outStack
- 如果outStack不为空，outStack弹出栈顶元素

本文首次发布于孙忠良 Blog, 作者 [@sunzhongliang] , 转载请保留原文链接.