算法是用于解决特定问题的一系列执行步骤,良好的算法可以为程序节省很多性能开销
本文演示代码为Swift语言
斐波那契数(fibonacci number)
求第n个斐波那契数
斐波那契数是后面的数字为前面两个数字的和
比如0 1 1 2 3 5 8 13…就是斐波那契数列
// 使用递归的算法计算斐波那契数
func fib(n: Int) -> Int {
if (n <= 1) { // n需要从1开始, 一直计算到1则停止计算,返回出去
return n;
}
// 前1个斐波那契数为:fib(n: n - 1)
// 前2个斐波那契数为:fib(n: n - 2)
return fib(n: n - 1) + fib(n: n - 2)
}
// 第6个斐波那契数列:0 1 1 2 3 5 8
print(fib(n: 6)) // 8
上述算法确实可以解决问题,但如果需要计算的斐波那契数很大呢,比如第40个数,将参数改为64,可以明显的看到在耗费了很长的时间之后控制台出现了:102334155
经过改进后的算法:
func fib2(n: Int) -> Int {
if (n <= 1) {
return n
}
var first = 0
var second = 1
for _ in 0..<n-1 {
// 思路:比如 0 1 1 2 3
// 第一个数为0,第二个数为1 后面的数为0+1
// 计算好0+1完成后,赋值给第二个数,第一个数=第二个数;依次往后推
let sum = first + second; // 这一次相加的结果要给second
first = second; // 第一个数给第二个
second = sum; // 当前相加的结果要给second
}
return second;
}
print(fib2(n: 64)) // 10610209857723
如何评价一个算法的好坏
时间复杂度(time complexity): 估算程序指令的执行次数(执行时间)
空间复杂度(space complexity): 估算所需占用的存储空间
复杂度
// 比如以下代码执行的复杂度就是1,因为执行条件只会进入一次
// 复杂度:1
func test(num: Int) {
if num > 10 {
print("num > 10")
}
else if num > 5 {
print("num > 5")
}
else {
print("num <= 5")
}
}
// swift当中的这种for循环,相当于OC当中的 for (int i=0; i<4; i++)
// int i = 0 复杂度1
// i<4 复杂度4
// i++ 复杂度4
// 4次print 复杂度4
// 复杂度:1 + 4 + 4 + 4
for n in 0..<4 {
print("test") // 里面的也要把复杂度计算上
}
// 复杂度:1 + 3n
func test2(len: Int) {
for n in 0..<len {
print("test2")
}
}
// 复杂度:1 + 2n + n * (1 + 3n)
// 3n² + 3n + 1
func test3(n: Int) {
for item in 0..<n {
for att in 0..<n {
print("test2")
}
}
}
// 复杂度:1 + 2n + n * (1 + 45)
// 48n + 1
func test4(n: Int) {
for i in 0..<n {
for j in 0..<15 {
print("test4")
}
}
}
// 这段代码的意思是n能除以多少次2 (依次取中间值)
// 比如:8 = 2^3 16 = 2 ^ 4
// 3 = log2(8) 4 = log2(16)
// 复杂度:log2(n)
func test5(n: inout Int) {
let con = n / 2
while con > 0 {
print("test5")
}
}
// 复杂度:1 + 2*log2(n) + log2(n) * (1 + 3n)
// 1 + 3*log2(n) + 2 * nlog2(n)
func test7(n: Int) {
// log2(n)
for var i in 1..<n {
i += i
// 里面的复杂度: 1 + 3n
for j in 0..<n {
print("test")
}
}
}
上面的复杂度表示起来还是有点复杂,有没有更简单的表示法呢?
大O表示法(Big O)
一般用大O表示法来描述复杂度,它表示的是数据规模n对应的复杂度
忽略常数、系数、低阶, 如:
9 表示 O(1)
2n + 3 表示O(n)
n² + 2n + 6 表示O(n²)
4n³ + 3n² + 22n + 100 表示O(n³)
在写法上面,n³相同于n^3
大O表示法仅仅是一种粗略的分析模型,是一种估算,能帮助我们短时间了解一个算法的执行效率
常见的复杂度
| 执行次数 | 复杂度 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 4n²+2n+6 | O(n²) | 平方阶 |
| 4log₂n+2 | O(logn) | 对数阶 |
| 3n+2nlog₃n+12 | O(nlogn) | nlogn阶 |
| 3n³+3n²+2n+1 | O(n³) | 立方阶 |
| 2ⁿ | O(2ⁿ) | 指数阶 |
在性能上比较:
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)
斐波那契数复杂度分析
回过头来看看使用递归算法计算的斐波那契数的复杂度是多少
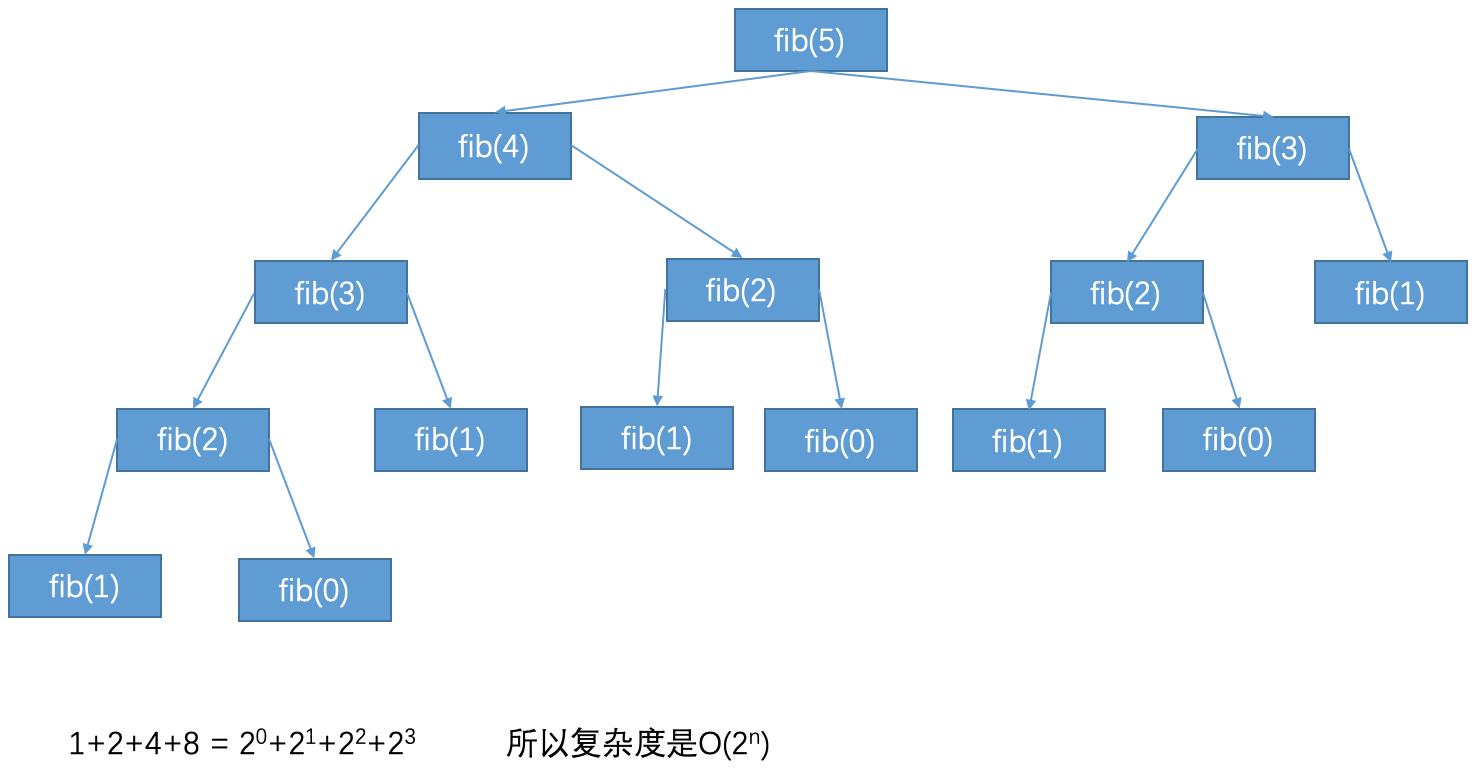 而用
而用非递归方式实现的斐波那契数复杂度是:O(n)
算法的优化方向
- 用尽量小的存储空间
- 用尽量少的执行步骤(执行时间)
- 特殊情况,灵活操作
- 空间换时间
- 时间换空间
本文首次发布于 孙忠良 Blog, 作者 [@sunzhongliang] , 转载请保留原文链接.